Mathematical Study for the Dynamical Behavior of Toxoplasmosis Disease in A Population

Abstract

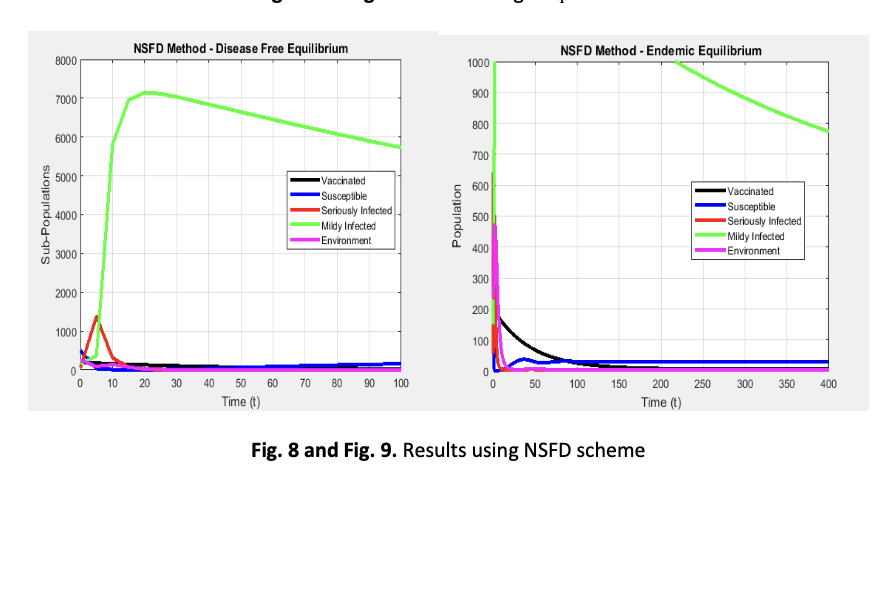
Mathematical modelling provides meaningful insight into infectious disease dynamics. Toxoplasmosis is protons parasitic disease caused by Toxoplasma gundi which is present in cat’s contamination, uncooked meat, polluted soil, water etc. which is risky for the people with weak immune system especially risky for the pregnant women. Due to silent nature and persistency, it causes serious public health issues as well as in animals. The problems addressed in given study are the comprehensive understanding about the dynamics of the disease within animal by interaction with infected population and also contaminated environment. The aim of this research is to investigate the dynamical behavior the toxoplasmosis disease in a cat population by mathematically using the compartmental model. The model is the extension of classical SIR framework introducing the compartments vaccinated, susceptible, seriously infected, mild infected and environmental contamination. This model uses various parameters which biologically reflect many rates like vaccination rate, immunity loss rate, oocysts shedding rate etc. By analyzing model mathematically, equilibrium points are derived which further introduced the threshold, basic reproductive number which tells about the behavior of disease either it will spread, persist or die out from population. With the help of analytical methods, stability analysis of the model is performed. Additionally, for the reliability of the results the different numerical schemes are tested using different initial conditions and step sizes for positivity, boundedness and dynamical consistency. Mathematical foundation is presented by the given model for comprehend the most influencing factors on the toxoplasmosis disease transmission. To check whether there is endemic or pandemic case, threshold conditions are identified and impact of each parameter on the system dynamics is observed. Detailed conclusions are drawn for the sensitivity analysis. In conclusion many results are drawn concerning vaccination as control strategies to completely die out the disease from the population.