Modelling the Impact of Immune Response and Drug Intervention on Tumor Growth using Ordinary Differential Equation

Abstract

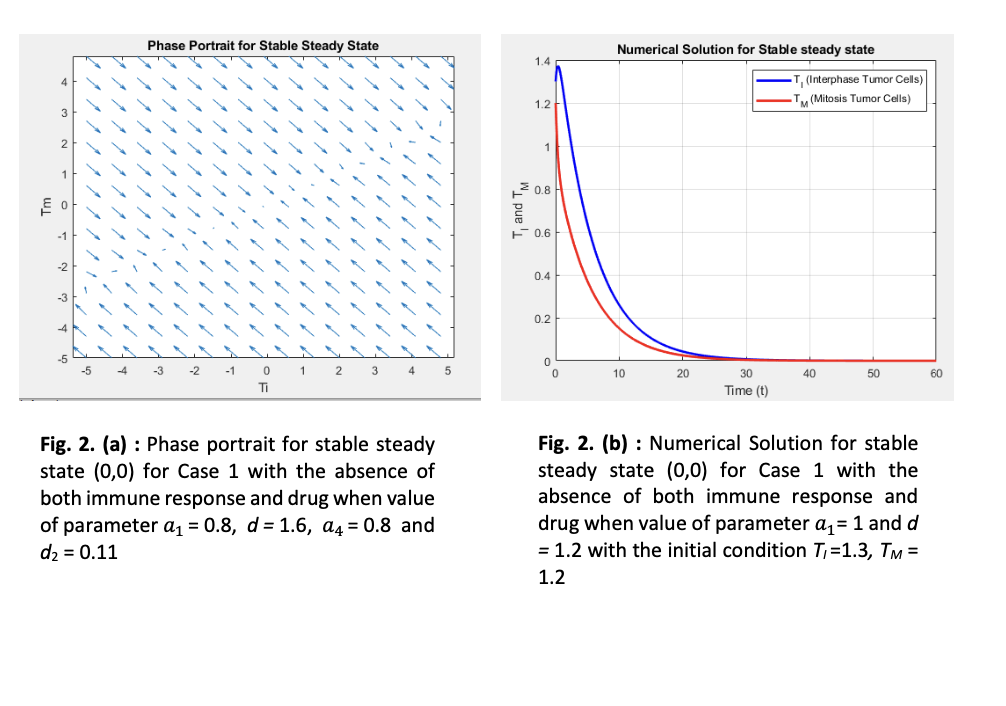
Cancer progression often occurs due to immune evasion and the limitations of conventional treatments such as chemotherapy, which may also damage healthy cells. Mathematical modelling provides a useful framework for understanding the interactions between tumor growth, immune response, and drug intervention. This study presents a mathematical model based on a system of ordinary differential equations to investigate how tumor growth is affected by immune response and chemotherapy. The study aims to develop mathematical models describing tumor-immune interactions, analyze their stability across three scenarios which is the absence of immune response and drug, presence of immune response without drug, and presence of both and conduct numerical simulations of tumor-immune-drug dynamics. Stability analysis is discussed for each case, with numerical simulations using the Runge-Kutta (RK4) method in MATLAB for selected parameters within the stability region. The findings demonstrate that combining immune response with drug intervention enhances tumor suppression compared to either approach alone.