Numerical Analysis of Lassa Fever Epidemic Model

Abstract

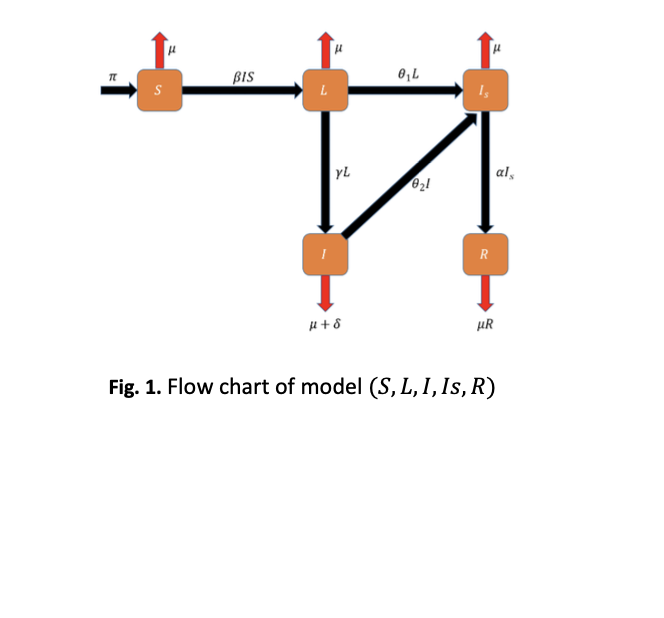
Lassa fever is an acute Hemorrhagic viral fever which is first discover in a town Lassa. In this paper we constructed a mathematical model to derive a relation of ordinary differential equations with saturated incident rate. Mathematical modelling is very useful tool in the field of epidemiology to study the behavior of diseases like COVID-19 Hepatitis B virus and Lassa fever etc. By using mathematical modeling, we analyze the existence and stability of the DFE and EE and find the Reproductive number . The disease-free equilibrium is locally stable if , and it is unstable if   and disease endemic points are stable if . The transmission dynamics of Lassa fever is analyzed numerically. In the present work two numerical schemes are developed which are standard finite difference (SFD) and non-standard finite difference scheme (NSFD). SFD scheme give conditionally convergence and do not behave well for certain parameter h. Our main purposed is to developed Non-Standard Finite Difference (NSFD) scheme which is unconditionally convergent for the Lassa fever model. Furthermore, we discuss the stability analysis of NSFD scheme. Finally, numerical experiments with all three schemes are presented to investigate the theoretically results.