Modeling and Simulation of Unemployment Transitions using Computational Methods

Abstract

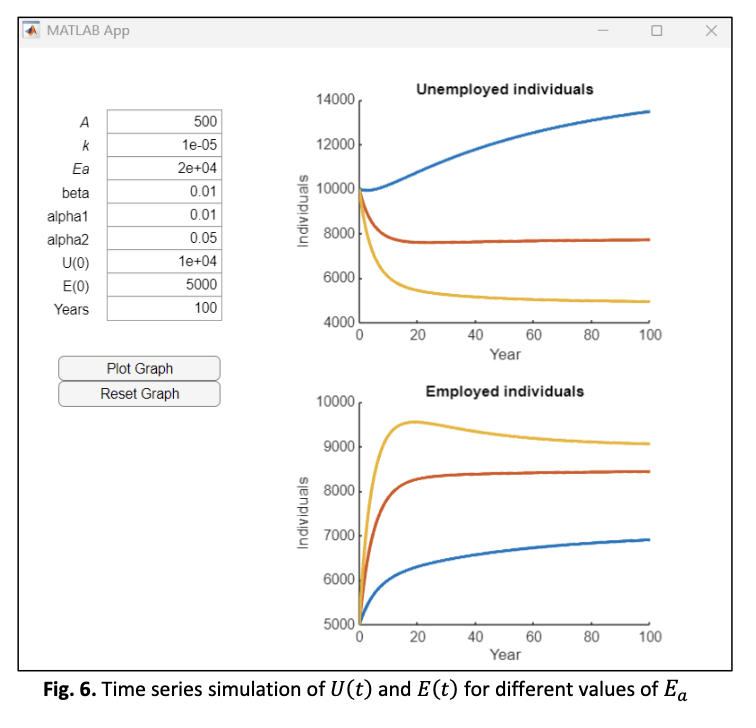
Unemployment affects both individuals and the economy, leading to social problems, poverty, and slower national development. To understand its dynamics, this paper studies a population model of employed and unemployed individuals using a system of ordinary differential equations. The adult population is divided into two groups: unemployed and employed individuals. The model includes parameters such as job vacancies, hiring rate, resignation rate, retirement rate, and death rate, which are theoretically defined to represent realistic labor transitions. The analysis shows that all population variables remain non-negative and bounded over time. The stability of the equilibrium point is examined using Descartes’ rule of signs and the Routh-Hurwitz criteria. Numerical simulations and a MATLAB graphical user interface are employed to illustrate how parameter variations affect unemployment and employment levels. The results show that increasing job opportunities reduces unemployment, while higher resignation rates worsen it. These findings can help policymakers identify which factors most strongly influence unemployment dynamics.