Hesitant Fuzzy B-Spline Modeling: A New Approach to Quintic Spatial Curve Approximation Model

Abstract

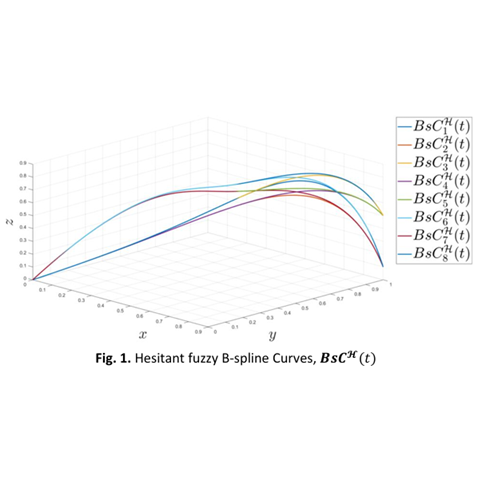
Fuzzy geometric modeling has been applied in various fields, where the fuzzy set approach allows the representation of uncertainty for better visualization. In fact, numerous types of fuzzy sets, including the traditional fuzzy set, type-2 fuzzy set, and intuitionistic fuzzy set, among others, are successfully applied in geometric modeling, while there is a gap in representing hesitancy, which often occurs during data collection. The hesitant fuzzy set provides a method to represent hesitancy—in other words, all opinions on the data through different membership degrees assigned to each element. This paper aims to introduce a novel model, namely the hesitant fuzzy B-spline curve approximation model. The study starts with a comprehensive literature review on the development of fuzzy geometric modeling. By applying the fundamental concepts of the hesitant fuzzy set and hesitant fuzzy control point relation defined, the hesitant fuzzy B-spline curve approximation model is constructed. A numerical example of hesitant fuzzy quintic B-spline spatial curves is visualized through the model. The study demonstrates an effective and flexible method to represent uncertainty through hesitancy, which will advance the field of fuzzy geometric modeling.